From Philosophy to Geometry: Descartes’ Legacy and the Art of Batik
“I think, therefore I am,” or in Latin, “Cogito ergo sum,” is one of the most famous quotes by the French philosopher René Descartes. He argued that while everything else could be doubted—such as sensory perception and physical reality—the very act of doubting confirms the existence of a thinking entity. This quote illustrates Descartes' brilliance in logical reasoning and his use of syllogism, earning him a place as one of philosophy's most prominent figures. But did you know his genius also extended into mathematics?
As a mathematician, he was a prolific writer. When we are in school, we are introduced to a coordinate system called “Cartersian Coordinate”. This coordinate is named after him, whose contribution in Math especially in analytical geometry earned him the honour to be named as one of the most used coordinate systems in the world.
In this article, we’ll explore one of Descartes’ lesser-known theorems and use it to create a new Batik pattern. Known as the theory of kissing circles, this concept was discussed in his correspondence with Princess Elisabeth of the Palatinate—a royal scholar and student of Descartes. In their exchange, Descartes tackled an ancient mathematical puzzle about four mutually tangent circles, a problem that had puzzled mathematicians for millennia.
The following text will provide a geometrical perspective on Batik Kawung, outline its mathematical formula, and guide you in manually drawing it using a compass and ruler or digitally with SVG code. Then, we’ll learn about Descartes’ theorem and apply it to design new Batik motifs. Finally, we’ll take the pattern a step further by integrating it into the design of a necklace pendant for jewelry.
The Geometry Behind the Beauty
Batik Kawung is one of the oldest and most iconic motifs in Java. This motif appears frequently in Indonesian temple statues, adorning figures like Mahakala in the Singosari temple, as well as Ganesha, Nandishvara, and Durga Mahishasuramardini. Over centuries, the Kawung motif has endured as a cultural emblem. Today, it remains a prevalent design in Indonesian textiles, architecture, and even popular culture. If you look closely, you’ll spot it in unexpected places, such as the opening credits of the 2013 Studio Ghibli animated movie The Tale of Princess Kaguya .
Given its timeless appeal, the Kawung motif invites deeper exploration, particularly its geometric foundation. Among its many interpretations, we focus on the circular Kawung. This form is defined by the intersection of four equal circles positioned around the origin: one above at (0, -r), one below at (0, r), one to the left at (-r, 0), and one to the right at (r, 0), as illustrated in the figure 1
Drawing Kawung by Hand: A Step-by-Step Guide
Knowing how to sketch Batik Kawung manually using a pencil, a compass, and paper is a relatively straightforward process. Given a square ABCD, we can draw a circle centered at O with a radius equal to half of the square's side length. Next, we draw a quarter circle centered at vertex A. We then draw a quarter circle at vertices B, C, and D as shown in figure below.
-
Given square ABCD, draw a circle centered at O with a radius equal to half of the square side length.
-
Draw a quarter circle centered at vertex A, using the same radius.
-
Repeat step #2 three times, centering the quarter circles at vertices B, C, and D, respectively.
Using the steps mentioned above, we are able to draw the main motive “klowongan” of Batik Kawung. To make it more visually pleasing, batik artists usually add secondary motives and background motives. Secondary motive is usually called “isen-isen”. Isen-isen is the decorative fillings found within the main patterns. These additional motifs are used to fill the spaces between the main motifs to enhance the overall aesthetic appeal of the fabric. For batik Kawung, usually isen cecek are used. The illustration of this concept can be found in the figure below.
Mastering Digital Kawung: Step-by-Step Instructions
If we only want to draw hand written batik, then it is enough to only know how to draw it manually using the steps mentioned above. However, if we want to use computers to generate digital patterns for digital printing or 3D modeling design, we need to represent Batik in a way that computers understand. One of those ways is to represent Kawung in Scalable Vector Graphic (SVG).
Scalable Vector Graphics (SVG) is an XML-based markup language for describing two-dimensional based vector graphics. The benefit of using SVG is that the image can be rendered at any size and it will still look clean. The other benefit is that SVG format is easily readable by 3D modeling CAD programs. For instance, if we want to make a necklace pendant with motif Kawung, we can import an SVG file of Kawung and extrude it in a 3D modeling CAD program. To draw Kawung using Scalable Vector Graphic, we can write the following code in a text editor.
<g transform="translate(x_origin, y_origin)">
<path d="M0 0 A R R 0 0 1 R R A R R 0 0 1 0 0"></path>
<path d="M0 0 A R R 0 0 1 R R A R R 0 0 1 0 0" transform="rotate(90)"></path>
<path d="M0 0 A R R 0 0 1 R R A R R 0 0 1 0 0" transform="rotate(180)"></path>
<path d="M0 0 A R R 0 0 1 R R A R R 0 0 1 0 0" transform="rotate(270)"></path>
</g>
The explanation of the code mentioned above are as follows:
First, we group four path elements inside a group tag, we then change the coordinate of the group to the origin we wanted. Second, we draw a path that describes the leaf of the Kawung. To describe the leaf, we use attribute d in the path and use the following command.
<path d="M0 0"></path> → Move cursor to the origin (0,0)
<path d="A R R 0 0 1 R R"></path> → Using Arc command to draw an arc from (0,0) with radius-x equals to R, radius-y equals to R, 0 degree x-axis rotation, 0 large-arc-flag (it determines that arc should be less than 180 degrees), 1 sweep flag (means clockwise) to end coordinate (R,R).
<path d="A R R 0 0 1 0 0"></path> → Using Arc command draw an arc from (R,R) back to starting coordinate (0,0).
The same arc command is then used three times, the resulting path is then rotated 90 degrees to get the shape of Kawung.
Descartes Theorem and Apollonian Gasket
Descartes theorem is crucial to the development of Apollonian Gasket. Apollonian Gasket is a type of circle fractal, in which every circle is tangent to three other circles. We are going to substitute the circle with a Kawung shape to make a pattern author named as Apollonian Kawung Gasket. Descartes theorem is needed to find the radius, and the coordinate of the circle center
Descartes theorem is used to get the radius and location of the circle center, given that we know three others mutually tangent circle position and radius. The first circle C1, is a circle located at position (0,0) and radius r1 let’s say 140. The second one is located at (-70,0) and has radius r2 = 70. The third circle is located at (70,0) and has radius r3 = 70. Using Descartes' theorem we can find the radius of the fourth circle and the location of the circle centre. To solve this problem, we can use the following formula:
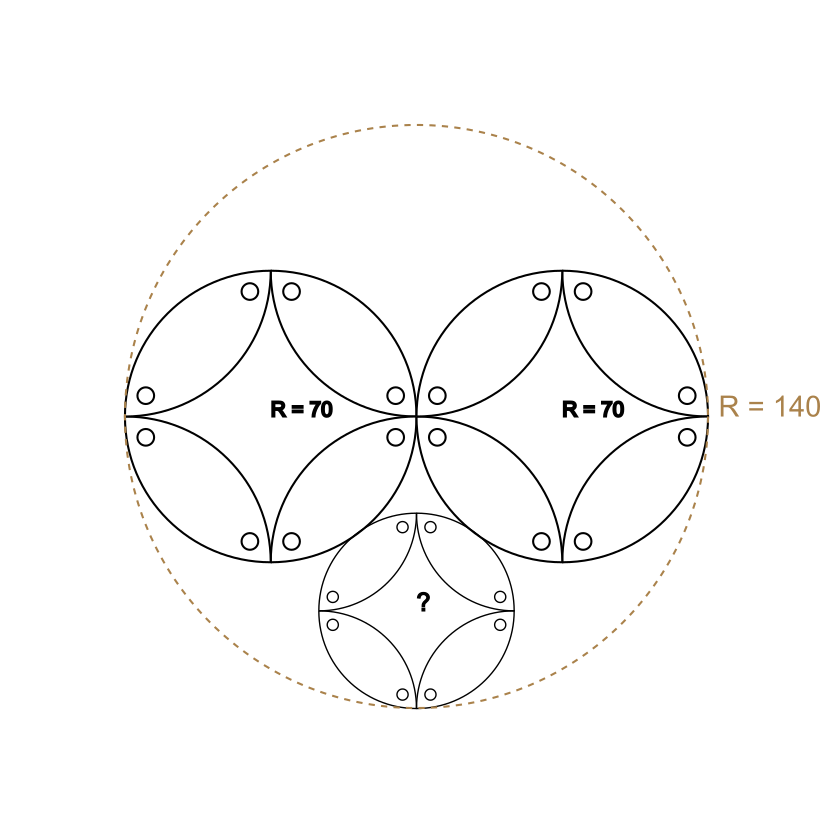
\( (k_1 + k_2 + k_3 + k_4)^2 = 2 \cdot (2k_1 ^2 + k_2 ^2+ k_3 ^2 + k_4 ^2) \)
To get the location of circle's center, we can use complex Descartes theorem:
\( (k_1 z_1 + k_2 z_2 + k_3 z_3 + k_4 z_4)^2 = 2 \cdot (2k_1 ^2 z_1 ^ 2+ k_2 ^2 z_2^2+ k_3 ^2 z_3 ^ 2 + k_4 ^2 z_4 ^ 2) \)
To draw intricate patterns, we will apply Descartes' theorem multiple times. While this process could be done manually, it would be a laborious task. Instead, we can use recursion to make the process more efficient. Recursion is a technique where a function calls itself to solve a problem. In this case, we will create a recursive function that calculates the fourth circle given three circles. This function will continue to call itself until the radius of the newly created circle falls below a set threshold. Below is the pseudocode for this recursive approach:
circleList = []
def recursiveDescartes(circle1, circle2, circle3):
circle4 = calculate(circle1, circle2, circle3)
circleList.append(circle4)
if circle4.r > threshold:
recursiveDescartes(circle1, circle2, circle4)
recursiveDescartes(circle2, circle3, circle4)
recursiveDescartes(circle1, circle3, circle4)
Bringing Kawung to Life: Creative Applications
Using Descartes' theorem that we have learned in this chapter, we can create a variety of creative products. For instance, this mathematical concept can inspire designs for T-shirts, tumblers, and book covers, among others. Below are examples of images you can generate using the principles covered in this chapter. These designs not only showcase the elegance of mathematics but also demonstrate the versatility of geometric art in everyday items.

Not only can we decorate products with 2D SVG designs, but we can also create 3D objects. One of the most exciting applications is designing a necklace pendant. The process is surprisingly simple. First, import the SVG file into a 3D CAD program like Blender. Next, convert the design elements into a mesh. Then, apply a solidify modifier to extrude the design and add thickness. Finally, export the model as an .STL file. Once ready, you can send it to a 3D printing jewelry service such as Sculpteo, Materialise, or Shapeways. And voilà—your custom necklace pendant is ready to wear or gift! Below is a 3D render showcasing the final design.

References
Codepen by @pimskie: How to draw Apollonian Gasket on HTML Canvas using Javascript